Bab kali ini akan dibahas mengenai penarikan kesimulan
silahkan di perhatikan
Dalam logika matematika ada tiga model penarikan kesimpulan yang sah, yaitu modus ponens, modus tolens, dan silogisme.
model 1:
Diketahui premis-premis berikut.
premis (1) : p —> q
premis (2) : p
kesimpulan : q
pola penarikan kesimpulan argumentasi di atas adalah modus ponens.
Diketahui premis-premis berikut.
premis (1) : p —> q
premis (2) : p
kesimpulan : q
pola penarikan kesimpulan argumentasi di atas adalah modus ponens.
model 2:
Diketahui premis-premis berikut.
premis (1) : p —> q
premis (2) : -q
kesimpulan : -p
pola penarikan kesimpulan argumentasi di atas adalah modus tolens.
Diketahui premis-premis berikut.
premis (1) : p —> q
premis (2) : -q
kesimpulan : -p
pola penarikan kesimpulan argumentasi di atas adalah modus tolens.
model 3:
Diketahui premis-premis berikut.
premis (1) : p —> q
premis (2) : q —> r
kesimpulan : p —> r
pola penarikan kesimpulan argumentasi di atas adalah silogisme.
Diketahui premis-premis berikut.
premis (1) : p —> q
premis (2) : q —> r
kesimpulan : p —> r
pola penarikan kesimpulan argumentasi di atas adalah silogisme.
Perlu diketahui kadangkala soal yang diberikan harus diolah dahulu sehingga kita dapat menarik kesimpulan.
Ingat bahwa p —> q ekivalen dengan -p v q ekivalen juga dengan -q —> -p.
Ingat bahwa p —> q ekivalen dengan -p v q ekivalen juga dengan -q —> -p.
copy soal dari un 2006/2007
Persoalan 1:
Diketahui premis-premis berikut:
1. Jika Budi rajin belajar maka ia menjadi pandai.
2. Jika Budi menjadi pandai maka ia lulus ujian.
3. Budi tidak lulus ujian.
Kesimpulan yang sah adalah….
a. Budi menjadi pandai.
b. Budi rajin belajar.
c. Budi lulus ujian.
d. Budi tidak pandai.
e. Budi tidak rajin belajar.
Persoalan 2:
Premis (1): Jika Fadhil lulus ujian pegawai atau menikah maka ayah memberi hadiah uang.
Premis (2): Ayah tidak memberi hadiah uang.
Kesimpulan yang sah adalah….
a. Fadhil tidak lulus ujian dan menikah.
b. Fadhil tidak lulus ujian pegawai dan tidak menikah.
c. Fadhil lulus ujian pegawai atau menikah.
d. Fadhil tidak lulus ujian pegawai atau tidak menikah.
e. Jika Fadhil tidak lulus ujian pegawai maka Fadhil tidak menikah.
Premis (1): Jika Fadhil lulus ujian pegawai atau menikah maka ayah memberi hadiah uang.
Premis (2): Ayah tidak memberi hadiah uang.
Kesimpulan yang sah adalah….
a. Fadhil tidak lulus ujian dan menikah.
b. Fadhil tidak lulus ujian pegawai dan tidak menikah.
c. Fadhil lulus ujian pegawai atau menikah.
d. Fadhil tidak lulus ujian pegawai atau tidak menikah.
e. Jika Fadhil tidak lulus ujian pegawai maka Fadhil tidak menikah.
Persoalan 3:
Penarikan kesimpulan yang sah dari argumentasi berikut:
Jika Siti sakit maka dia pergi ke dokter.
Jika Siti pergi ke dokter maka dia diberi obat.
Adalah…
a. Siti tidak sakit atau diberi obat.
b. Siti sakit atau diberi obat.
c. Siti tidak sakit atau tidak diberi obat.
d. Siti sakit dan diberi obat.
e. Siti tidak sakit dan tidak diberi obat.
Penarikan kesimpulan yang sah dari argumentasi berikut:
Jika Siti sakit maka dia pergi ke dokter.
Jika Siti pergi ke dokter maka dia diberi obat.
Adalah…
a. Siti tidak sakit atau diberi obat.
b. Siti sakit atau diberi obat.
c. Siti tidak sakit atau tidak diberi obat.
d. Siti sakit dan diberi obat.
e. Siti tidak sakit dan tidak diberi obat.
Persoalan 4:
Dari argumentasi berikut:
Jika adik tidak makan, maka adik tidak bertenaga.
Jika adik tidak bertenaga maka dia lemas.
Kesimpulan yang sah adalah….
a. Adik tidak makan atau adik lemas.
b. Adik makan atau adik lemas.
c. Adik makan atau adik tidak lemas
d. Adik tidak makan walaupun lemas.
e. Adik bertenaga karena makan.
Dari argumentasi berikut:
Jika adik tidak makan, maka adik tidak bertenaga.
Jika adik tidak bertenaga maka dia lemas.
Kesimpulan yang sah adalah….
a. Adik tidak makan atau adik lemas.
b. Adik makan atau adik lemas.
c. Adik makan atau adik tidak lemas
d. Adik tidak makan walaupun lemas.
e. Adik bertenaga karena makan.
Persoalan 5:
Diketahui pernyataan:
1. Jika hari panas, maka Ani memakai topi.
2. Ani tidak memakai topi atau ia memakai payung.
3. Ani tidak memakai payung.
Kesimpulan yang sah adalah….
a. Hari panas.
b. Hari tidak panas.
c. Ani memakai topi.
d. Hari panas dan Ani memakai topi.
e. Hari tidak panas dan Ani memakai topi.
Diketahui pernyataan:
1. Jika hari panas, maka Ani memakai topi.
2. Ani tidak memakai topi atau ia memakai payung.
3. Ani tidak memakai payung.
Kesimpulan yang sah adalah….
a. Hari panas.
b. Hari tidak panas.
c. Ani memakai topi.
d. Hari panas dan Ani memakai topi.
e. Hari tidak panas dan Ani memakai topi.
Persoalan 6:
Diketahui premis-premis berikut:
Premis 1: Jika Dodi rajin belajar, maka ia naik kelas.
Premis 2: Jika Doi naik kelas, maka ia akan dibelikan baju.
Kesampulan yang sah adalah….
a. Dodi tidak rajin belajar tetapi ia akan dibelikan baju.
b. Dodi rajin belajar tetapi ia tidak akan dibelikan baju.
c. Dodi rajin belajar atau ia akan dibelikan baju.
d. Dodi tidak rajin belajar atau ia akan dibelikan baju.
e. Dodi rajin belajar atau ia tidak akan dibelikan baju.
Diketahui premis-premis berikut:
Premis 1: Jika Dodi rajin belajar, maka ia naik kelas.
Premis 2: Jika Doi naik kelas, maka ia akan dibelikan baju.
Kesampulan yang sah adalah….
a. Dodi tidak rajin belajar tetapi ia akan dibelikan baju.
b. Dodi rajin belajar tetapi ia tidak akan dibelikan baju.
c. Dodi rajin belajar atau ia akan dibelikan baju.
d. Dodi tidak rajin belajar atau ia akan dibelikan baju.
e. Dodi rajin belajar atau ia tidak akan dibelikan baju.
Persoalan 7:
Diketahui premis-premis:
(1) Jika Dinda rajin belajar, maka ia menjadi pandai.
(2) Jika Dinda menjadi pandai, maka ia lulus ujian.
(3) Jika Dinda lulus ujian, maka ia bahagia.
Kesimpulan yang sah adalah…
a. Jika Dinda rajin belajar maka ia tidak bahagia.
b. Jika Dinda rajin belajar maka ia bahagia.
c. Jika Dinda menjadi pandai maka ia rajin belajar.
d. Jika Dinda tidak rajin belajar, maka ia tidak bahagia.
e. Jika Dinda tidak menjadi pandai, maka ia rajin belajar.
q : saya minum di kelas
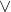 q : saya makan atau minum di kelas
q : saya makan atau minum di kelas
p q : jika saya makan di kelas maka saya minum di kelas
q : jika saya makan di kelas maka saya minum di kelas
~ p : saya tidak makan di kelas.
 q
q
 q
q
 q
q
Diketahui premis-premis:
(1) Jika Dinda rajin belajar, maka ia menjadi pandai.
(2) Jika Dinda menjadi pandai, maka ia lulus ujian.
(3) Jika Dinda lulus ujian, maka ia bahagia.
Kesimpulan yang sah adalah…
a. Jika Dinda rajin belajar maka ia tidak bahagia.
b. Jika Dinda rajin belajar maka ia bahagia.
c. Jika Dinda menjadi pandai maka ia rajin belajar.
d. Jika Dinda tidak rajin belajar, maka ia tidak bahagia.
e. Jika Dinda tidak menjadi pandai, maka ia rajin belajar.
Contoh 1:
p : saya makan di kelasq : saya minum di kelas
p 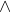 q : saya makan di kelas dan saya minum di kelas (disingkat: saya makan danminum di kelas)
q : saya makan di kelas dan saya minum di kelas (disingkat: saya makan danminum di kelas)
p p
~ p : saya tidak makan di kelas.
Modus Ponens dan Modus Tollens sebenarnya adalah teknik penarikan kesimpulan dari logika manusia juga. Di Logika Matematika, kedua teknik penarikan kesimpulan tersebut dinyatakan dengan:
Modus Ponens
p
p
———
Kesimpulan: q
———
Kesimpulan: q
Modus Tollens
p
¬ q
———
Kesimpulan: ¬ p
———
Kesimpulan: ¬ p
Arti Modus Ponens adalah “jika diketahui p  q dan p, maka bisa ditarik kesimpulan q“. Sedangkan Modus Tollens berarti “jika diketahu p
q dan p, maka bisa ditarik kesimpulan q“. Sedangkan Modus Tollens berarti “jika diketahu p  q dan ¬q, maka bisa ditarik kesimpulan ¬p“.
q dan ¬q, maka bisa ditarik kesimpulan ¬p“.
Contoh 2:
Diketahui cerita sederhana berikut: Jika saya makan di kelas maka saya minum di kelas. Saya makan di kelas. Apakah saya minum di kelas?
Solusi:
Menggunakan Contoh 1 di atas, kita memperoleh kalimat matematika:
p Menggunakan Contoh 1 di atas, kita memperoleh kalimat matematika:
p
Menggunakan Modus Ponens, maka kita bisa menarik kesimpulan q, yang artinyasaya minum di kelas.
—————- []
Contoh 3:
Diketahui cerita sederhana berikut: Jika saya makan di kelas maka saya minum di kelas. Saya tidak minum di kelas. Apakah saya makan di kelas?
Solusi:
Menggunakan Contoh 1 di atas, kita memperoleh kalimat matematika:
Menggunakan Contoh 1 di atas, kita memperoleh kalimat matematika:
p  q
q
¬q
¬q
Menggunakan Modus Tollens, maka kita bisa menarik kesimpulan ¬p, yang artinyasaya tidak makan di kelas.
—————- []
Contoh 4:
Diketahui cerita sederhana berikut: Jika saya makan di kelas maka saya minum di kelas. Jika saya minum di kelas maka ruangan kelas menjadi kotor. Saya makan di kelas. Apakah ruangan kotor?
Solusi:
Misalkan:
p : saya makan di kelas
q : saya minum di kelas
r : ruangan kelas menjadi kotor
q : saya minum di kelas
r : ruangan kelas menjadi kotor
maka, cerita sederhana tersebut dapat dinyatakan dengan
1: p  q2: q
q2: q  r3: p
r3: p
Menggunakan Modus Ponens untuk kalimat 1 dan kalimat 3, maka kita bisa menarik kesimpulan q, yang artinya saya minum di kelas. Kalimat-kalimat matematikanya bisa kita ubah menjadi:
1: p  q2: q
q2: q  r3: p4: q
r3: p4: q
Dengan menggunakan Modus Ponens untuk kalimat 2 dan 4, kita memperoleh kesimpulan r, yang artinya ruangan kelas menjadi kotor.
—————- []
Contoh 5:
Diketahui cerita sederhana berikut: Jika saya makan maka saya tidak belajar. Jika televisi sedang mati maka saya belajar. Saat ini, televisi sedang mati. Apakah saya sedang makan?
Solusi:
Misalkan:
p : saya makan
q : saya belajar
r : televisi mati
q : saya belajar
r : televisi mati
maka, cerita sederhana tersebut dapat dinyatakan dengan
1: p  ¬q2: r
¬q2: r  q
q
3: r
3: r
Kesimpulan dengan Modus Ponens untuk kalimat 2 dan kalimat 3: q.
Kalimat matematika diubah menjadi:
Kalimat matematika diubah menjadi:
1: p  ¬q2: r
¬q2: r  q
q
3: r4: q
3: r4: q
Dengan menggunakan Modus Tollens untuk kalimat 1 dan kalimat 4, kita peroleh kesimpulan ¬p, yang artinya saya tidak makan.
—————- []
Cerita di contoh-contoh di atas adalah sederhana. Namun bukan berarti contoh yang lebih kompleks tidak bisa diselesaikan dengan teknik ini. Berikut adalah contoh dengan cerita yang lebih kompleks.
Contoh 6:
Diketahui cerita berikut: Pak Ali biasa ke kantor menggunakan mobil. Tentu saja jika mobilnya tidak mengalami masalah. Kalau mobilnya punya masalah, dia akan menggunakan angkutan umum. Biasanya dia mengetahui bahwa mobilnya punya masalah saat mau berangkat, menyebabkan dia terlambat tiba di kantor. Tetapi dia juga bisa terlambat meskipun naik mobil karena jalannya macet. Gara-gara terlambat, dia tidak bisa menghabiskan kopinya, yang sudah disediakan di dapur kantor. Pagi ini terlihat kopinya sudah habis. Pertanyaan:
a. Apakah mobil pak Ali bermasalah?
b. Apakah jalanan macet?
a. Apakah mobil pak Ali bermasalah?
b. Apakah jalanan macet?
Solusi:
Misalkan:
p : mobil Pak Ali bermasalah
q : Pak Ali ke kantor naik mobil
r : Pak Ali ke kantor naik angkutan umum
s : Pak Ali terlambat
t : Jalanan macet
u : Kopinya Pak Ali habis.
q : Pak Ali ke kantor naik mobil
r : Pak Ali ke kantor naik angkutan umum
s : Pak Ali terlambat
t : Jalanan macet
u : Kopinya Pak Ali habis.
maka, cerita tersebut dapat dinyatakan dengan
1: p  r2: ¬p
r2: ¬p  q3: r
q3: r  s4: q Λ t
s4: q Λ t  s5: s
s5: s  ¬u
¬u
6: u
6: u
Kesimpulan yang bisa diambil:
7: ¬s {Modus Tollens dari 5 dan 6}
8: ¬r {Modus Tollens dari 3 dan 7}9: ¬p {Modus Tollens dari 1 dan 8}
8: ¬r {Modus Tollens dari 3 dan 7}9: ¬p {Modus Tollens dari 1 dan 8}
Arti kalimat 9: mobil Pak Ali tidak bermasalah (Jawaban untuk pertanyaan a).
Kesimpulan untuk menjawab pertanyaan b:
Kesimpulan untuk menjawab pertanyaan b:
10: q {Modus Ponens dari 2 dan 9}11: ¬(q 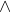 t) {Modus Tollens dari 4 dan 7}12: ¬q
t) {Modus Tollens dari 4 dan 7}12: ¬q 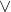 ¬t {Hukum de Morgan untuk 11}13: q → ¬t {Ekuivalensi implikasi dengan 12}14: ¬t {Modus Ponens dari 10 dan 13}
¬t {Hukum de Morgan untuk 11}13: q → ¬t {Ekuivalensi implikasi dengan 12}14: ¬t {Modus Ponens dari 10 dan 13}
Kalimat 14 berarti Jalanan tidak macet (Jawaban untuk pertanyaan b).
—————- []
Catatan Tambahan:
Hukum de Morgan:
¬(p 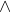 q) ≡ (¬p
q) ≡ (¬p 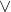 ¬q)
¬q)
¬(p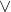 q) ≡ (¬p
q) ≡ (¬p 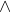 ¬q)
¬q)
¬(p
Ekuivalensi implikasi:
(p  q) ≡ (¬p
q) ≡ (¬p  q)
q)
Tidak ada komentar:
Posting Komentar